You need to convert 50 km h^-1 to m s^-1

50 km h^-1 = 50 000 m ÷ 3600 s = 14 m s^-1

Assume the mass of a car is 1500 kg

KE = 1 /2 m v²

KE = 1 / 2 x 1500 x (14)² = 147 000 J is rounded 1.5 x 10⁵ J

Answer B is correct.

The resistance of 100 cm wire = 10 Ω → R branch RST = 10 Ω

The resistance of 50 cm wire = 5 Ω → R branch RT = 5 Ω

The resistance of 25 cm wire = 2.5 Ω → R branch XR = 2.5 Ω and R branch TY = 2.5 Ω

The circuit can be considered to be built up as shown below:

R between R and T : ` 1/R = 1/5 + 1/10`

→ ` 1/R = 2/10 + 1/10 = 3/10`

R between R and T `= 10/3 = 3.3 Ω`

R between X Y = 2.5 Ω + 3.3 Ω + 2.5 Ω = 8.3 Ω

Answer C is correct.

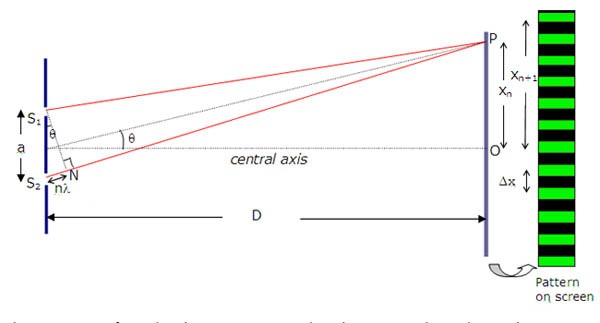
A double slit experiment is shown below.

A maximum at X_n on the screen will be formed when the difference in distance travelled by light from slit 1 and travelled from slit 2 = n λ (= n wavelengths).

The 2 waves arriving from slit 1 and slit 2 are in phase.

This distance (n λ) is shown in the diagram below in the small triangle close to the slits.

In this triangle the following relation is applicable:

`sin θ = n λ/a`
(1) (a is the distance between the centres of the slits)

In the triangle of the central axis the following relation is applicable:

`tan θ = X_n/D` (2)

If θ is small (smaller than 15 ^o) then sin θ is nearly equal to tan θ.

(sin 15^o = 0.26 and tan 15^o = 0.27)

Combining (1) and (2) →

`n λ/a = X_n/D` → `X_n = n λ D/a` (3)

(this relation (3) is not exact, but an acceptable approximation)

From relation (3) can be concluded:

The distance between fringes is proportional to

1. the wavelength λ of the light and
2. the distance D between the slits and the screen.

However, the distance between the fringes is inversely proportional to the separation a of the slits.

Answer A is wrong. The distance between the light source and the slits does not affect the distance between the fringes.

The correct answer is B: increasing the distance between the slits and the screen will increase the distance between the fringes.

Answer C is wrong. If the distance between the slits increases the distance between the fringes will decrease.

Answer D is wrong. The wavelength is smaller at a higher frequency and this will decrease the distance between the fringes.

The length of the spring unstretched is 1.0 cm.

When the length is increased from 2.0 cm to 3.0 cm the extension is increased from 1.0 cm to 2.0 cm. The stretching force increases then from 2.0 N to 4.0 N (see

diagram).

The increase in strain energy = the work done = area under graph from extension 1.0 cm to 2.0 cm.

This area is a trapezium with base 4.0 N and height 1.0 cm.

This area is also equal to a rectangle with base 3.0 N (= the average force) and height 1.0 cm.

See the diagram below.

The average force `= (2.0 N + 4.0 N)/2 = 3.0 N`

W done =3.0 N x 1.0 x 10^-2 m = 0.030 J

Increase in strain energy = 0.030 J .

Answer B is correct.